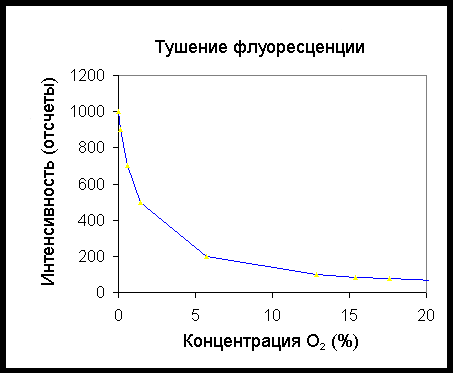
В волоконно-оптических кислородных зондах Ocean Optics используется флуоресцентный метод измерения парциального давления кислорода. Излучение синего (~ 475 нм) светодиода передается в зонд по оптическому волокну и возбуждает флуоресценцию специально подобранного химического комплекса, внедренного в тонкослойное золь-гелевое покрытие на конце зонда. Гидрофобная золь-гелевая матрица эффективно удерживает флуоресцирующий комплекс и защищает его от воды. Возбужденный комплекс флуоресцирует в видимой области спектра с максимумом вблизи 600 нм. При столкновении с молекулой кислорода происходит безызлучательная передача избыточной энергии, что приводит к уменьшению, или тушению, сигнала флуоресценции (см. ниже «Тушение флуоресценции»). Степень тушения зависит от концентрации кислорода в золь-гелевом покрытии, которая находится в динамическом равновесии с концентрацией кислорода в образце. Излучение флуоресценции собирается зондом и по оптическому волокну передается в спектрометр. Полученный спектр и данные его обработки отображаются в программе OOISensors.

Тушение флуоресценции

Кислород, будучи триплетной молекулой, способен эффективно тушить флуоресценцию и фосфоресценцию некоторых люминофоров. Этот эффект (впервые описанный Каутским в 1939 г.) называется «динамическим тушением флуоресценции». Столкновение молекулы кислорода с флуорофором в возбужденном состоянии приводит к безызлучательной передаче энергии. Степень тушения зависит от частоты столкновений, а следовательно, от концентрации, давления и температуры кислородсодержащей среды.

Калибровка

Для выполнения точных количественных измерений кислородный зонд необходимо откалибровать. Процедура калибровки зависит от того, в каких условиях предполагается использовать зонд.

Определите, нужно ли вводить поправку на изменение температуры образца. В общем случае температура влияет на скорость затухания и интенсивность флуоресценции, частоту столкновений молекул кислорода с флуорофором и коэффициент диффузии кислорода. Для получения максимально точных результатов следует поддерживать образец при постоянной температуре (отклонения не более ±3 °C). Подробнее о температурной компенсации см. здесь.
2. Выберите алгоритм калибровки. Линейный алгоритм Штерна-Фольмера требует как минимум двух стандартных образцов с известной концентрацией кислорода, тогда как полиномиальный алгоритм второго порядка требует не менее трех таких образцов.

Результатом выполнения выбранного алгоритма является калибровочная кривая, позволяющая рассчитывать концентрацию кислорода в неизвестных образцах. Алгоритм второго порядка дает более точную кривую, что обеспечивает более высокую точность измерений, особенно при работе в широком диапазоне концентраций.

Линейный алгоритм Штерна-Фольмера

Алгоритм Штерна-Фольмера требует как минимум двух стандартных образцов с известной концентрацией кислорода. Первый образец должен иметь нулевую концентрацию (0%). Концентрация во втором образце должна соответствовать верхней границе диапазона, в котором предстоит работать. Зависимость интенсивности флуоресценции на выходе зонда от парциального давления кислорода выражается уравнением Штерна-Фольмера: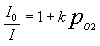

где:

I₀ — интенсивность флуоресценции при нулевом давлении кислорода;
I — интенсивность флуоресценции при давлении p;
k — постоянная Штерна-Фольмера.

Постоянная Штерна-Фольмера (k) зависит главным образом от химического состава флуорофора. Зонды Ocean Optics показали высокую стабильность во времени, поэтому для них эта величина почти не должна зависеть от других компонентов измерительной системы. Однако у разных зондов постоянная Штерна-Фольмера будет отличаться, и кроме того, она зависит от температуры. Все измерения должны проводиться при той же температуре, при которой выполнялась калибровка. В противном случае следует измерять температуру и вводить соответствующую поправку.

Температурная зависимость величин в уравнении Штерна-Фольмера выражается следующим образом:

I₀ = a₀ + b₀ * T + c₀ * T²
k = a + b * T + c * T²

Интенсивность флуоресценции при нулевом давлении кислорода (I₀) зависит от конкретной оптической конфигурации: мощности светодиода, пропускания оптических волокон, потерь света в соединении зонда с волокном и обратного рассеяния в образце. Эту интенсивность нужно обязательно измерять при каждом изменении конфигурации.

Из уравнения Штерна-Фольмера следует, что наибольшая чувствительность зонда достигается при низких концентрациях кислорода. Фотометрическое отношение сигнал/шум примерно пропорционально квадратному корню из интенсивности сигнала. Скорость изменения сигнала при изменении концентрации будет наивысшей при малых концентрациях. Отклонения от уравнения Штерна-Фольмера наблюдаются главным образом при высоких концентрациях. Скорректировать эти отклонения можно при помощи полиномиального алгоритма второго порядка.

Обратное рассеяние в среде может повысить наблюдаемую интенсивность флуоресценции, поэтому при работе с сильно рассеивающими средами необходимо выполнять калибровку в той среде, где будут проводиться измерения. Для оптически прозрачных жидкостей и газов это не обязательно.

Полиномиальный алгоритм второго порядка

Этот алгоритм требует как минимум трех образцов с известной концентрацией кислорода. Первый образец должен иметь нулевую концентрацию, а последний — концентрацию, соответствующую верхней границе диапазона, в котором предстоит работать. В отличие от линейного алгоритма Штерна-Фольмера, для которого достаточно всего двух образцов, алгоритм второго порядка потенциально обеспечивает более высокую точность. Он определяется следующим уравнением: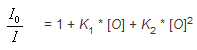

где:

I₀ — интенсивность флуоресценции при нулевом давлении кислорода;
I — интенсивность флуоресценции при давлении p;
K₁ — первый коэффициент;
K₂ — второй коэффициент.

Температурная зависимость величин, входящих в уравнение второго порядка, имеет следующий вид:

I₀ = a₀ + b₀ * T + c₀ * T²
K₁ = a₁ + b₁ * T + c₁ * T²
K₂ = a₂ + b₂ * T + c₂ * T²

Закон Генри

Систему, откалиброванную для газа, можно использовать для измерений в жидкости, и наоборот. В теории, сигнал кислородного зонда зависит только от концентрации кислорода. Связь между парциальным давлением и концентрацией дается законом Генри, который гласит, что при постоянной температуре масса газа, растворенного в жидкости, пропорциональна давлению этого газа на поверхность жидкости. Следовательно, давление газа над раствором пропорционально концентрации газа в растворе. Эта концентрация (в мольных процентах) может быть вычислена, если известно абсолютное давление:

мольная доля O₂ = парциальное давление O₂ / абсолютное давление

Поскольку зонд реагирует на концентрацию кислорода, при выполнении закона Генри сигнал в газовой среде будет подобен сигналу в жидкости, находящейся в равновесии с газом. Это позволяет использовать калибровку для газа при измерениях в жидких образцах, и наоборот. Однако закон Генри нельзя применять к газам, имеющим экстремально высокую растворимость в воде.

Ниже приводятся данные по растворимости кислорода в воде при различных температурах. В диапазоне 0...75 °C растворимость зависит от температуры следующим образом:

ln(X) = a + b/T* + cln(T*),

где:

X — мольная доля кислорода в воде;
T* = T/100 (в кельвинах);
a = ?66.7354; b = 87.4755; c = 24.4526.

T (C)	T* (T/100K)	Мольная доля кислорода в воде при 1 атм 0₂	Массовая доля (ppm) при 1 атм O₂	Массовая доля (ppm) при 0.209476 атм 0₂ (воздух)
5	2.7815	3.46024E-05	61.46203583	12.87482142
10	2.8315	3.06991E-05	54.52891411	11.42249881
15	2.8815	2.75552E-05	48.94460474	10.25272002
20	2.9315	2.50049E-05	44.41468119	9.303809756
25	2.9815	2.29245E-05	40.71933198	8.529722785
30	3.0315	2.12205E-05	37.69265242	7.895706058
35	3.0815	1.98218E-05	35.20817214	7.375267068
40	3.1315	1.86735E-05	33.16861329	6.948028438

Рассеивающие среды

Излучение флуоресценции распространяется во всех направлениях. Если окружающая среда прозрачна, зонд собирает только то излучение, которое испущено в направлении оптического волокна в пределах его угла зрения. Если же конец зонда расположен вблизи отражающей поверхности или погружен в сильно рассеивающую среду, то регистрируемый сигнал флуоресценции возрастает. Приращение сигнала пропорционально интенсивности флуоресценции как в присутствии, так и в отсутствии кислорода, и не влияет на постоянную Штерна-Фольмера. По этой причине необходимо измерять интенсивность флуоресценции при нулевом давлении кислорода в образце. Для достижения максимальной точности при измерениях в сильно рассеивающей среде, калибровка зонда должна выполняться в этой же среде.

Литература

Wang, W.; Reimers, C.E.; Wainright, S.C.; Shahriari. M.R.; Morris, M.J. «Applying Fiber-Optic Sensors for Monitoring Dissolved Oxygen» Sea Technology, March 1999, Vol. 40, No. 3, pp. 69–74.
Shahriari, M.R.; Murtaugh, M.T.; Kwon, H.C. Ormosil «Thin Films for Chemical Sensing Platforms» Chemical, Biochemical and Environmental Fiber Sensors IX, 1997, SPIE, Vol. 3105, pp. 40-51.
Krihak, M.; Shahriari, M.R. «A Highly Sensitive, All Solid State Fiber Optic Oxygen Sensor Based on the Sol-gel Coating Technique» Electronic Letters, 1996, Vol. 32, No. 3.
Krihak, M.; Murtaugh, M.T.; Shahriari, M.R. «Fiber Optic Oxygen Sensors Based on the Sol-Gel Coating Technique» Chemical, Biochemical and Environmental Fiber Sensors VIII, 1996, SPIE, Vol. 2836.
Allen, C.B.; Schneider, B.K.; White, C.J. «Limitations to oxygen diffusion in invitro cell exposure systems in hyperoxia and hypoxia» American Journal of Physiology Lung Cell Molecular Physiology, 281: L1021-L1027, 2001.